Learn how to make Half Square Triangles from Strips. There are so many cool ways to make Half Square Triangles and half square triangles from a jelly roll are super easy and really neat. Plus, it totally puts those jelly rolls to good use. Which is awesome because I always end up wanting to make some kind of quilt out jelly rolls that doesn't seem like it would work.

It would be so easy to make cute little pinwheels out of a jelly roll with this method, which is great because jelly rolls have so many different prints of each fabric collection.
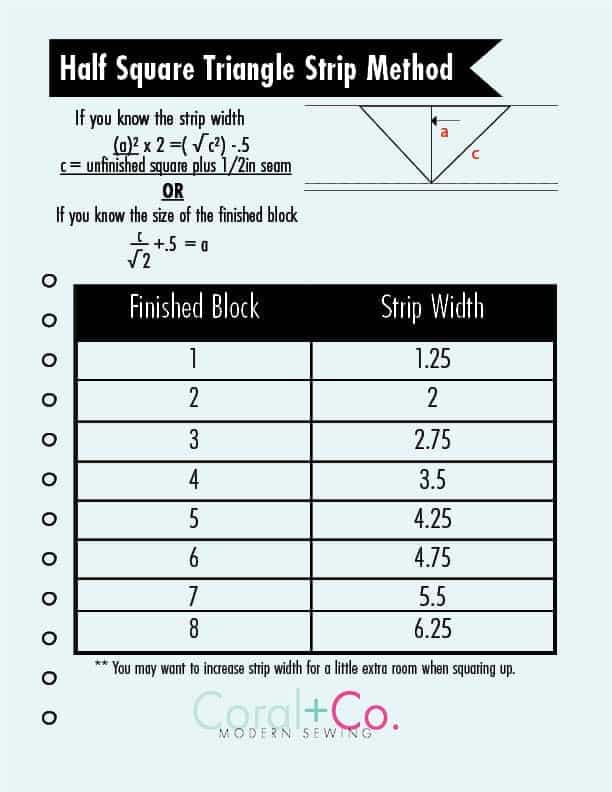
I've also included a half square triangle chart for making half square triangles from a jelly roll using the math formulas to figure out how to use the strip method.
This is the fourth installment of the Half Square Triangle Series. You can see the rest of the Half Square Triangle Series below:
- Method I - Simple Half Square Triangle Tutorial
- Method II - HST Tutorial 4 at a Time
- Method III - The Magic 8 Method - Make 8 HST at Once
- Method IV - Half Square Triangles from Strips - Use a Jelly Roll for Half Square Triangles!
- Method V - How to Use Half Square Triangle Paper
- 25+ Half Square Triangle Quilt Patterns
Tutorial: How to Make Half Square Triangles from Strips
You will want to be careful when handling these half square triangles with this method because they will be cut on the bias and more prone to stretch and distort when pressing and handling. For this tutorial, we will be sewing 2.5" Strips to make 2.5" unfinished half square triangles which will be 2" finished half square triangles.
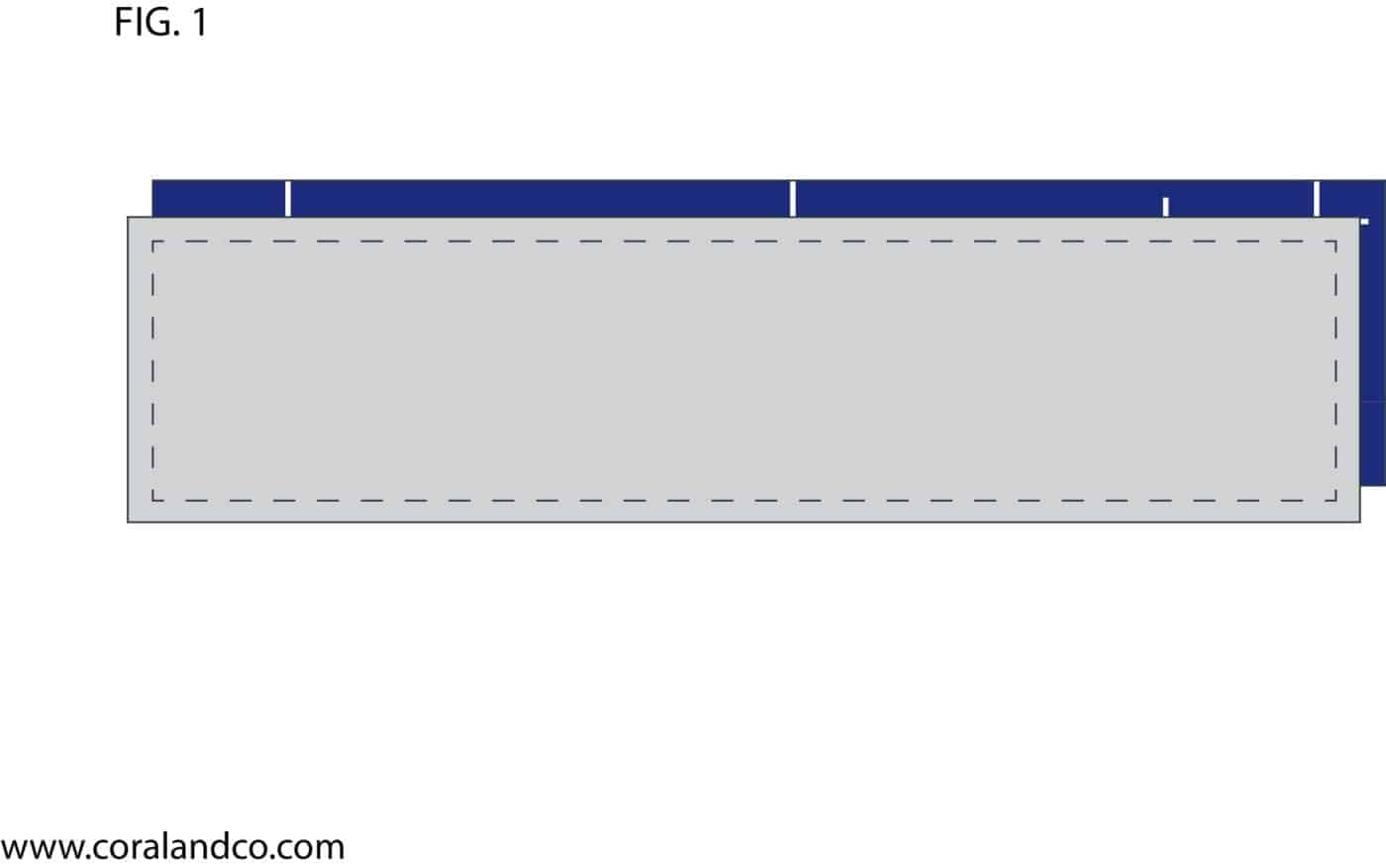
Step 1 - Place two jelly roll strips Right Sides Together and sew 1/4" down the long edges. You can sew around the entire tube if you would like since you will be discarding the edge pieces.
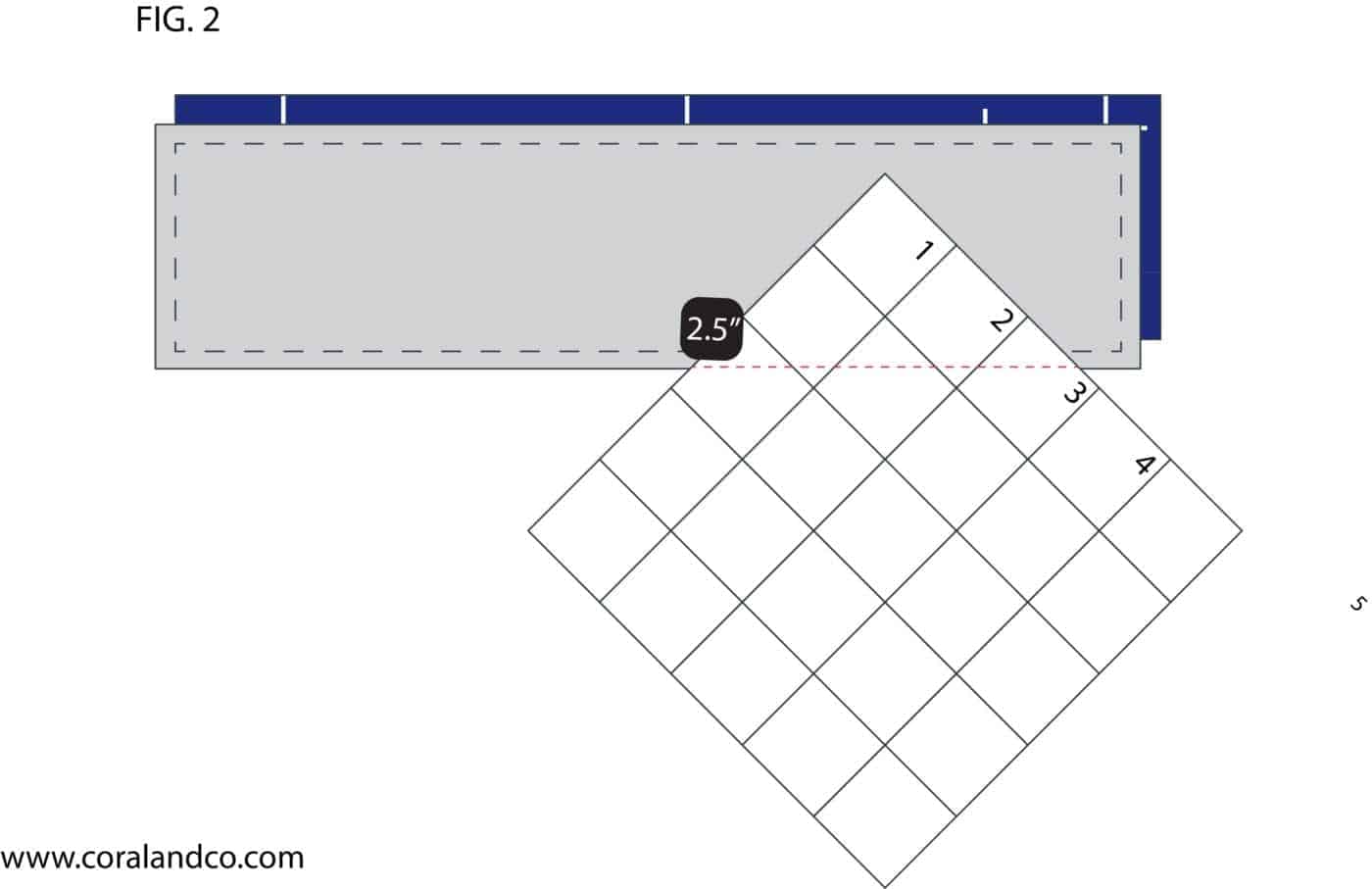
Step 2 - Line the ruler with unfinished size marking of the HST needed on the 1/4" stitch line. So, in this case, the 2.5" marking of the ruler will be on the 1/4" seam. The ruler will be at a 45-degree angle. Then cut out the fabric around the ruler.
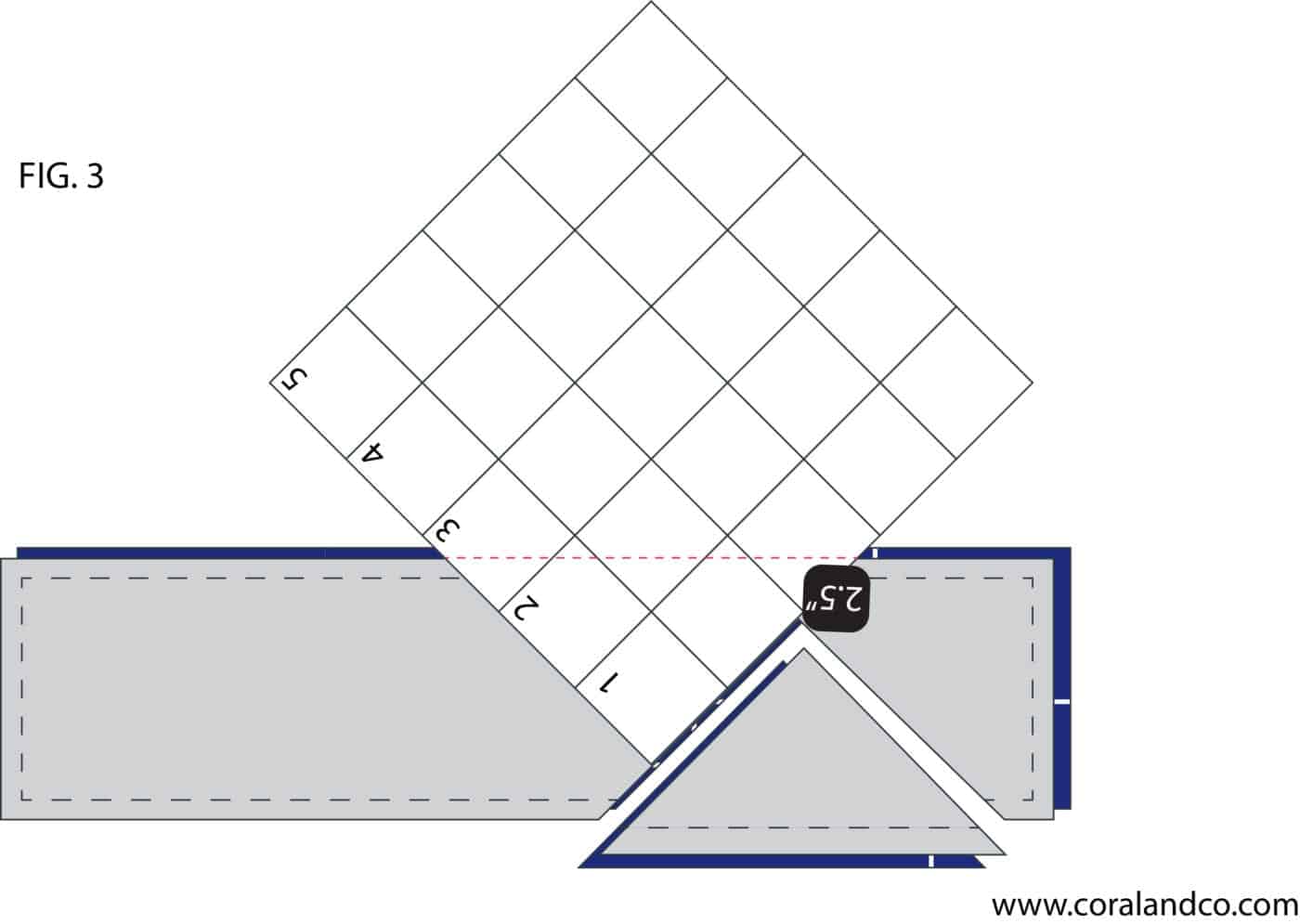
Step 3 - Rotate ruler to the opposite side of the strip lining up with the previous triangle cut and repeat the same steps as above.
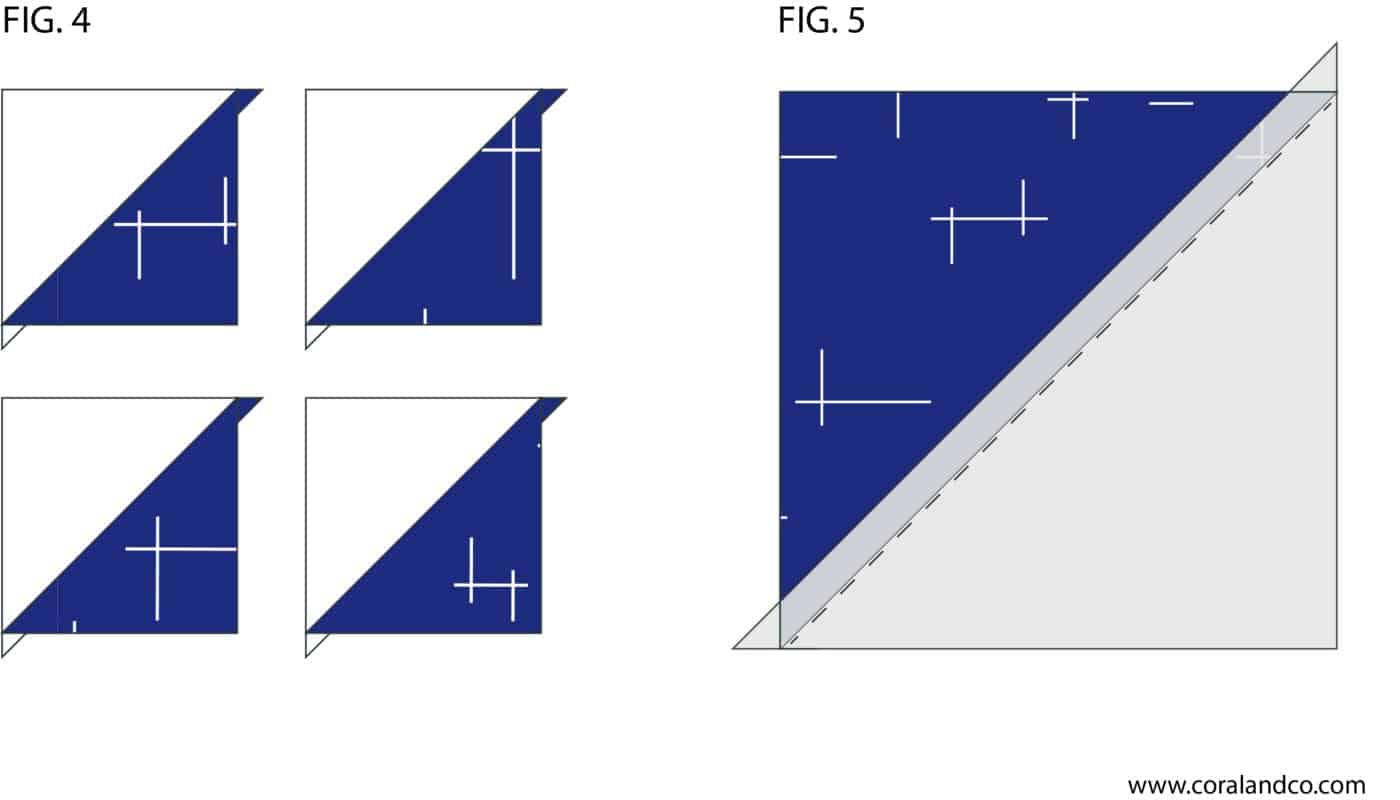
Step 4 - Open the blocks outward and either lightly finger press or use your iron to lightly press. Be very careful to only press up and down, NOT back and forth so as not to stretch them.
Step 5 -. Your seam should be pressed (both layers) toward the darker color.
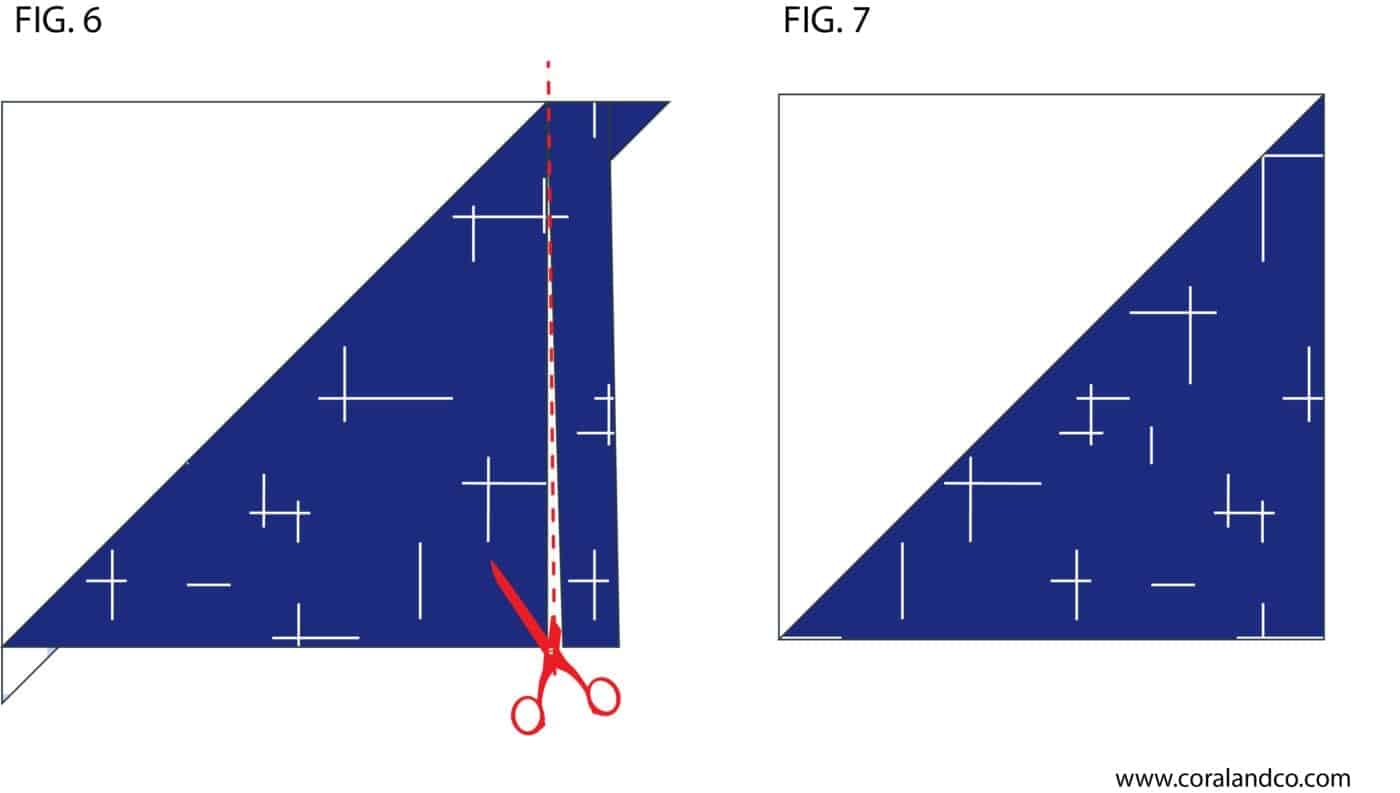
Step 6 - Place a ruler on the block keeping the 45-degree diagonal line over the diagonal seam. Trim each side of your square to the desired size.
Step 7 - Super Duper Easy!!!! You now have finished half square triangle blocks ready to assemble in a quilt top.
HALF SQUARE TRIANGLES FROM A JELLY ROLL FORMULA MATH
Here is a handy cheat sheet for half square triangles from a jelly roll math formulas. You can either use the dimensions given or use the formula to figure out your own dimensions.
- To figure out your own dimensions for making half square triangles from a jelly roll you will need to know either how wide the jelly roll strip width is or the size of the finished block you will need.
- Using the finished size half square triangle you would like, for instance, 3 inches, you take C or length of the finished block divided by the square root of 2 plus .5 inches for the seam allowance. This will give you the width of jelly roll strip to cut.
- If you know the strip width, say 2 inches, for example, you will take A or the strip width, square it and multiply it times 2. that will then equal the square root of C (or finished block size) squared. Take that number and subtract .5 or 1/2 inch seam allowance.
- You can use the chart given below to find the correct measurements. Some of these measurements are exact and leave very little room for error so I would add a little extra seam allowance or room to square up.
Learn How to Quilt Series
- How to Chain Piece Quilt Blocks
- How to Use a Rotary Cutter and Mat
- How to Choose the Right Machine Quilting Needle
- How to Use Half Square Triangle Paper


Very nice I like it project.
I will be starting it for my angel.
Thanks
Thank you!
What a wonderful way to make half square triangles. Thank you.
I was excited about this until you went into the algebra. This makes absolutely no sense to me, but I am not a mathematician.
I’m sorry to confuse you. I only gave the formula if you need to figure out your own specific block sizes that are not listed in the chart. Otherwise just use the measurement in the chart.
Thank you!
Hi from across the pond where is your chart please ? I’m wondering how many HST I can get from a jelly roll, I’m using an iPad if that makes a difference ??